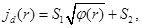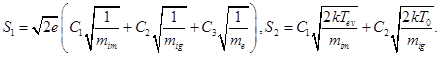Past Issues
The Mathematical Model of Arc Discharge in Metal Vapors at Active Gases over Crucible for Technological Process of Electron Beam Deposition of Ceramic Coatings
Igor Melnyk1*, Vitaliy Melnyk2, Serhii Tuhai1, Iryna Shved1, Dmytro Kovalchuk3
1National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”, Electronic Faculty, Electronic Devices and Systems Department, Kyiv, Ukraine
2National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”, Institute of Electronics and Microsystem Technique, Kyiv, Ukraine
3Joint Stock Company, Scientific and Industrial Association “Chervona Hvylia”, Kyiv, Ukraine
*Corresponding author: Igor Melnyk, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”, Electronic Faculty, Electronic Devices and Systems Department, Kyiv, Ukraine. e-mail: [email protected]
Citation: Melnyk I. (2022). The Mathematical Model of Arc Discharge in Metal Vapors at Active Gases over Crucible for Technological Process of Electron Beam Deposition of Ceramic Coatings. Nanoparticle 3(1):7.
Received : December 4, 2021 Published : January 10, 2022
Copyright: Melnyk I. © (2022).
ABSTRACT
The mathematical model of arc discharge in the metal vapors, propagated in the soft vacuum in the medium of active gases, is presented in this chapter. Such type of discharge is widely used in advanced electron beam technologies for obtaining the coating of new types from nanostructurized materials, especially ceramics coating. As electron beam sources for evaporation of refractory metals in this technological process the high voltage glow discharge electron guns are widely and effectively used. But the aim of applying of additional low-voltage arc discharge under the crucible is stimulating and maintaining the chemical reactions between metal vapors and residual gas in the vacuum technological chamber. In formed model for calculation of electric field distribution the analytical solving of Poisson equation is used, and the spatial distribution of discharge current density is defined on the base of the equation of uncontineously of electrons and ions flows. All analytical relations for auxiliary geometry of electrodes system with cylindrical crucible and ring electrode with positive potential over it have been obtained. Such electrodes system is standard for electron beam installations, designed to deposition of chemically complex ceramic coatings. The simulation results shown, that for power of electron beam range of nearly 10 kW and greater, the pressure in technological chamber range of few Pa and potential on electrode, located over crucible, 70 – 100 V, the current density of arc discharge is in range 0.05 – 0.1 А/cm2 . Such value of current density is generally enough to maintaining the chemical reaction between the metal vapors and active gas for obtaining the nanostructurized coatings with good steheometry. Obtained simulation results may be interesting to experts on applying of electron beam technologies for obtaining different types of nanostructurized ceramics coatings.
Keywords: Physical Vapor Deposition, Reactive Evaporation, Nanostructurized Ceramics Coatings, Electron Beam Evaporation, Arc Discharge, High Voltage Glow Discharge, Residual Gas
INTRODUCTION
Today in the technologies of obtaining the nanostructurized ceramic thin films is widely used the reactive deposition. The main physical processes of reactive films deposition are heating of evaporated metals by the powerful electron beam and propagation of metals vapor in the medium of active gases with lighting and maintaining the arc discharge. The distinguishing feature of such evaporation process is that in ionized plasma of arc discharge can take place such specific chemical reactions, which maintaining in the ordinary conditions, without gas ionization, is impossible. By applying such advanced electron beam technologies of films deposition can be obtained the perfect nanostructurized ceramic coatings with unique properties. Obtaining of such kind of chemical compound at the ordinary conditions, without additional ionization of metal vapors and technological gases in the arc discharge, is impossible. For example, obtaining of titanium nitride and titanium carbide films possible only at the conditions of reactive evaporation [1 – 4].
Since the traditional electron guns with heated cathodes can’t long time stably operated at the medium of active gases, often for providing the reactive deposition of ceramic thin films applied the high voltage glow discharge electron guns (HVGDEG). Generally, such guns are always characterized by the simplicity of construction, cheapness of the gun and evacuation equipment, as well as by the stable operation in the soft vacuum, range of 1 – 10 Pa, at the medium of active gases [5, 6]. In additional, effective control of beam power both by changing the operation pressure at the gun chamber [7] and by lighting the additional low-voltage discharge [8] is also possible.
Advanced technology of obtaining nanostructurized ceramic coatings with using HVGDEG can be successfully applied for many industrial applications in mechanical engineering, automotive industry, aerospace industry, as well as instrument-making and in electronics industry. The ceramic films, obtained with applying reactive deposition by using HVGDEG as the source of electron beam, are usually characterized by the high mechanical strength, heat resistance, as well as by the good dielectric properties. Therefore, using of such ceramics films and coatings is very perspective at cutting instruments, as thermoinsulation coating in engines, as well as thin dielectric films in the modern electronic devices, including microwave devices for communication systems [9 – 11].
Unfortunately, further development of advanced technology of reactive deposition of thin films with using HVGDEG is hampered by the lack of precision and adequate mathematical models of this process. The absence of such kind mathematical model does not allow to elaborate effectively the electron beam technological equipment for reactive deposition of nanostructurized thin films. Since the basic principles of simulation of high voltage glow discharge (HVGD) electron sources generally have been considered at the paper [6], for forming the complex model of process of reactive deposition of thin films considering the basic principles of simulation the arc discharge in the metal vapors over the crucible is necessary. Therefore, the aim of this chapter is considering these basic physical principles for such kind of model, obtaining necessary analytical relations and analyzing obtained simulation results.
BASIC STATEMENT OF CONSIDERED PROBLEM
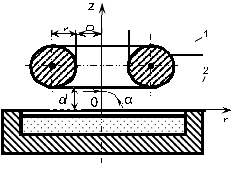
The generalized scheme of electrodes system for lighting and maintaining arc discharge in the metal vapors, which included surface of evaporated metal, located in crucible, and additional ring-like electrode with the positive potential relatively to crucible, is presented in Fig. 1 [5]. Basic geometry parameters of depicted at Fig. 1 electrodes’ system, which are necessary to forming the mathematic model, are presented at Fig. 2. On Fig. 2 the radius of cross-section of the ring electrode is noted as rr, the inner radius of ring – as Rr, the angle between axis z and the line, which connected the origin of coordinate system with the center point of ring – as α, and the distance between electrode and crucible as d. Corresponding to Fig. 2, the solving of considered task was provided in cylindrical coordinates system, and the origin of coordinates system is coincided with the center of upper base of cylindrical surface of crucible.
Fig. 1: Schematic view of electrodes’system to maintaining arc discharge. 1 – crucible, 2 – ring-like electrode, 3 – electron beam, 4 – vapor of evaporated materials, 5 – substrate
The mathematic model for simulation of electrodes system, presented schematically at the Fig. 2, is generally based on the following presumptions.
- Distribution of electric field between the ring-like electrode and the surface of evaporated metal is defined by analytical solving of Poisson Equation (PE) at the cylindrical coordinates.
- The value of space charge, which stand at the right side of PE, is defined by the equation of continuity for electrons and ions current.
- Energy of the metal’s atom at the upper base of crucible surface defined from the Boltzmann law as kTev.
- The vapor under the crucible can be considered as saturated. Corresponding to this assumption defined the concentration metal’s atoms nm.
- Concentration of atoms of residual gas is defined by pressure in technological chamber pg.
- Level of ionization of metal vapor atoms is defined by the coefficient of ionization βm.
- Level of ionization of residual gas atoms is defined by the coefficient of ionization βg.
- Corresponding to the model of single charged ions, the number of ions and electrons at the volume of arc discharge is considered as equal.
Fig. 2: Basic geometry parameters of considered electrodes’system to maintaining arc discharge. 1 – crucible, 2 – ring-like electrode
Basic equations, which are corresponded to described above physical presumptions of considered simulation problem, will be presented at the next sections of this chapter.
FORMING AND SOLVING OF BASIC EQUATION SYSTEM
Equations for calculation the distribution of electric field
Generally, the equation for defining of electric field at the electrodes system, which structure and geometry parameters are presented at Fig. 2, is follow from general form of Poisson equation at cylindrical coordinates:
where U(r,z) – the electric potential, ρ – space charge density [12, 13].
Analytical solving of equation (1) for electrodes system with the plane and thin-ring electrodes, like plotted at Fig. 2, is written as follows [12, 13]:
where ε – dielectric constant of residual gas, .png) – universal dielectric constant,
– universal dielectric constant, 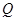 – space charge of elementary ring [12, 13]. Corresponded to equation (2), axial strength of electric is defined as [12, 13]:
– space charge of elementary ring [12, 13]. Corresponded to equation (2), axial strength of electric is defined as [12, 13]:
Defining the pressure of saturated vapor, concentration of metals’ atoms and necessary power of electron beam
The pressure of saturated vapor at the system of reactive deposition of cheremic films, which general constructive scheme is presented at Fig.1 and the geometry parameters are defined at Fig. 2, in the general case can be defined with using Mendeleev – Clapeyron equation as follows [14 – 16]:
where ps – pressure of saturated vapors, ρv – density of vapors, μv – molecular mass of vapors, 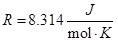 – universal gas constant, Tev – temperature of metals evaporation. Since the density of vapors ρv is always connected with molecular mass and pressure by the following relation [14 – 16]:
– universal gas constant, Tev – temperature of metals evaporation. Since the density of vapors ρv is always connected with molecular mass and pressure by the following relation [14 – 16]:
where .png) – Avogadro constant, pa – atmospheric pressure, the equation (4), taking into account (5), can be rewritten as follows:
– Avogadro constant, pa – atmospheric pressure, the equation (4), taking into account (5), can be rewritten as follows:
After mathematical transformers of the relation (6), the direct analytical expression for pressure of saturated vapors is simply written as follows:
In another hand, saturated pressure is connected with concentration of metals atoms nm by the following analytical relation [14 – 16]:
Therefore, taking into account relations (7) and (8), the analytical relation for concentration of the atoms of metal vapors over the crucible is written as follows:
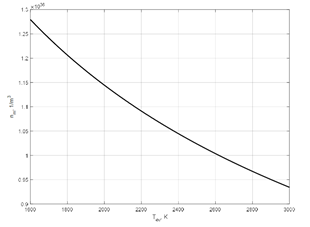
Concentration of metal’s atoms nm, have been defined with using the equation (9), is used later by substitution to the differential equation (1) for defining the space charge in simulated electrodes system of reactive deposition of thin films. Dependence nm(Tev), have been obtained with using relation (9) is presented at Fig. 3.
It is also important, that concentration of vapor atoms nm is strongly depended on power of electron beam and defined by simple relation [14 – 16]:
where qev – specific heat of vaporization, mm – mass of metal atoms.
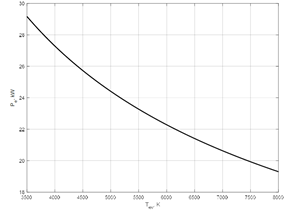
Taking into account relation (9), the dependence Pev(Tev) for obtaining the regime of saturation vapors, can be written as follows:
Dependence Pev(Tev), obtained with using relation (11) for titanium evaporation which have thermodynamic parameter .png) and
and .png) [17], is presented at Fig.4.
[17], is presented at Fig.4.
Fig. 3: Dependence of concentration of metal atoms in the system of reactive deposition of thin films on the temperature of metal vapors for titanium
Fig. 4: Dependence of necessary beam power on the temperature of titanium vapors
Defining the space charge in the system of reactive deposition of thin films on the base of equation of continuously the current of arc discharge
Let’s rewriting the equation (1) for considered electrodes system, applied for reactive deposition of ceramic coating, with taking into account relation for concentration of metals’ atoms (9) and other relations of gas dynamic [14 – 16]. Firstly, the current density of arc discharge has to be estimated on the base of fundamental relations of gas-discharge theory, presented in monographs [18 – 20]. Generally, the current density of arc discharge can be estimated as follows [18 – 20]:
where mim – mass of metal ions, mig – mass of gas ions, nim – concentration of metal ions, nig – concentration of gas ions, T0 – the temperature of environment, ne – concentration of electrons, me – mass of electrons.
For model of single-charge ionization, taking into account the law of charges equilibrium, such relation is always holds [18 – 20]:
Taking into account, that concentration of gas atoms is defined as [14 – 16]:
relation (13), with taking into account (9), (14), can be rewritten as:
where βm – level of ionization of metal vapor atoms, βg – level of ionization of gas atoms.
Therefore, equation (12), with taking into account (9, 14, 15), can be rewriting as follows:
For simplifying obtained equation (16) and further solving the differential equation (1), the following coefficient have been introduced:
With using substitutions (17), equation (16) has been rewritten in the simplified form as follows:
With known the spatial distribution of electrical potential φ(r), the current-voltage characteristic of considered arc discharge at the metal’s vapors can be obtained with using equation (18).
Now, for further analytical solving of differential equation (1), the components of obtained equation (18) for current density of metal ions jim, of residual gas ions’ jig and of electrons’ je, have to be considered separately. In such case, the following analytical relations should to be written:
It is also well-known fact, that the space charge, formed by the moving charged particles in the electrodes’ system, is defined form the current density of this particles by the following relations [12, 13, 18 – 20]:
where s – sort of the particles, vs – velocity of the particles, qs – charge of the particles.
Therefore, for obtaining the values of space charges, formed by the metals’ ions ρim, by the residual gas ions ρig and by the electrons ρe, corresponding to equations (19, 20), such analytical relations can be written:
Substituting coefficients C1, C2 and C3 from relations (17) to relations (21) and making corresponded analytical transformers, the following relations to the values of space charges of ions and electrons can be written as follows:
Taking into account the law of equilibrium of charged particles, defined by the relations (13, 17), from obtained relations (22), after corresponded mathematical transformers, the formula for summarized space charge ρΣ can be wrote as follows:
where
For further theoretical analysis, it is very important, that the coefficients of the model C1, C2, and C3 have been cancelled out and, thus, vanished from the set of equations (22, 23). Consequently, the values of these intermediate model coefficients, in any way, don’t affect to the potential distribution in the simulated electrode system. From a physical point of view, this fact can be explained by the compensation of the space charges of electrons and ions, which generally corresponds to the system of equations (17).
On the base of obtained relations (22, 23) the potential distribution in the considered electrodes system, which basic construction and main geometry parameters are presented at Fig. 1 and Fig. 2, can be defined by analytical solving the differential equation (1).
Defining the distribution of electric field
Taking into account the simple analytical relation (22), differential equation (1) can be written for the considered system of reactive deposition of thin films as follows:
where the constant K defined by the obtained analytical relation (23).
The initials conditions for Cauchy problem [21] for formulated task, corresponded to Fig. 2, can be written as follows:
Corresponded explanation draft is given at Fig. 5.
Fig. 5: Basic principle for defining the initial conditions for equation (24), corresponding to Fig. 2
Therefore, solution of equation (24), with taking into account the initial conditions (25), is follows:
where E0 and U0 – the constants, which are defined by initial conditions (25).
From the equations (25 – 27), such analytical relation to the value E0 can be written:
Taking into account obtained relation (28) and substitution the value of E0 into equation (27), following analytical relation can be obtained:
From obtained equation (29) the direct analytical relation for defining unknown value Ud from the basic discharge electric and geometry parameters is written as follows:
Taking into account obtaining relations (28, 30) for the coefficients E0 and U0, finally analytical relation (27) for the potential distribution φ(r) can be rewritten as follows:
Let assume in the equation (31) the following substitute:
After that substitution, formula (31) can be considered as standard cubic equation with the following coefficients:
Analytical solving of the set of equations (33) with using well-known Cordano formulas [22] give such result:
The simulation results for distribution of potential at the plane of ring electrode location, obtained with using relation (34), as well as results of calculation of current density distribution, will be presend at the next part of this chapter.
Simulation results and its analyze
The results of simulation of distribution the electris field U(r) at the plane of simmetry of ring electrode of simulated electrodes system, designed for reactive deposition of thin films at the soft vacuum, is presented at Fig. 6. These results have been obtained with using the set of equations (23, 34) for different values of arc discharge voltage Ud. These results was obtained for such dischartge parameters:
- The inner radius of ring electrode Rr = 0.05 m.
- Power of electron beam Pb = 20 kW.
- Pressure of residual gas at the technological chamber pg = 5 Pa.
- Level of ionization of metal vapor atoms βm = 0.8.
- Level of ionization of residual gas atoms βg = 0.75.
Fig. 6: Distribution of electric field at the symmetry plane of ring electrode for the simulated system of reactive deposition of thin films with maintaining arc discharge
Calculation was provided for evaporation of titanium at the medium of nitrogen, necessary empirical coefficients was taking from the references [17 – 21]. It is clear generaly, that obtaining the precision values for level of gas and vapors ionization, βg and βm, is also very sophysticated task. Usually level of ionization for different metals and gases is strongly depend on electron beam power, pressure in technological chamber and voltage of arc discharge mantaining [18 – 20]. In any case, obtained simulation results for distribution of electric field at the ring plane are looks plausible. Near the ring the potential of electric field is equal to value Ud and the derivation of potential 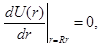 that fully corresponded to boundary conditions (25). Neary the symmetry axis of simulated electrode system the electric potential is always few Volts smaller, and generally the reducing of potential can be explained by the sagging of electric field at the ring plane. This physical effect is also described mathematically with using equations (2, 3) [12, 13]. For free space, without charged particles, and for the values of voltage at the ring electrode Ud range of 50 – 100 V, the sagging of electric field potential is generally grater, up to 15 – 20 V [12, 13]. Therefore, in the considered conditions of maintaining the arc discharge the smallest value of potential sagging near the axis of electrodes’ system can be explained by the influence of space charge of the positive ions of metal vapors and residual gas [18 – 20]. As for space charge of electrons, its influence in the discharge systems is always smaller by the reason of small mass of electrons and its high velocity and negligible [18 – 20]. Also, it is important on the theoretical point of view, that derivation of electric potential on the axis of electrodes system is also
that fully corresponded to boundary conditions (25). Neary the symmetry axis of simulated electrode system the electric potential is always few Volts smaller, and generally the reducing of potential can be explained by the sagging of electric field at the ring plane. This physical effect is also described mathematically with using equations (2, 3) [12, 13]. For free space, without charged particles, and for the values of voltage at the ring electrode Ud range of 50 – 100 V, the sagging of electric field potential is generally grater, up to 15 – 20 V [12, 13]. Therefore, in the considered conditions of maintaining the arc discharge the smallest value of potential sagging near the axis of electrodes’ system can be explained by the influence of space charge of the positive ions of metal vapors and residual gas [18 – 20]. As for space charge of electrons, its influence in the discharge systems is always smaller by the reason of small mass of electrons and its high velocity and negligible [18 – 20]. Also, it is important on the theoretical point of view, that derivation of electric potential on the axis of electrodes system is also  This important condition is always satisfied for axial electrodes systems [12, 13].
This important condition is always satisfied for axial electrodes systems [12, 13].
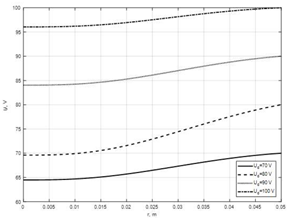
With known dependence of potential distribution at the plane of symmetry of ring electrode the value of current density of arc discharge can be defined with using equation (18). Corresponded graphic dependences, obtained as results of using described simulation technique, are presented at Fig. 7, a, b. The values of the coefficients C1 and C2 for considered parameters of arc discharge, pointed out above, was 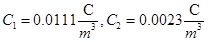 .
.
Fig. 7: Distribution of discharge current density jd at the symmetry plane of ring electrode for the simulated system of reactive deposition of thin films with maintaining arc discharge. The values of discharge voltage are: a) Ud = 90 V and Ud = 100 V; b) Ud = 70 V and Ud = 80 V
Clear, that generally dependences of arc discharge current density, presented at Fig. 7, similar to dependences of electric potential distribution, given at Fig. 6. This fact can be simply explained by analyzing and rewritten the equation (18). Really, dependence jd(φ(r)), defined with using equation (18), with knowing coefficients C1, C2 and C3, can be rewritten in the simplified form as follows:
Where
Therefore, as it is clear form dependences (35, 36), the dependence of current density on electric potential jd(φ(r)) defined by the constantly grows mathematic function  and namely by this reason the dependences jd(r), plotted at Fig. 7, and U(r), plotted at Fig. 6, are generally similar.
and namely by this reason the dependences jd(r), plotted at Fig. 7, and U(r), plotted at Fig. 6, are generally similar.
As a results of provided researches, main analytical dependences for pervious estimation the electrical parameters of arc discharge at the technological systems of reactive deposition of thin films, have been obtained and described in this chapter of book. For real systems of films deposition, which are put into operation at the industrial equipment, more precision values of model coefficients C1, C2, C3, K, S1 and S2, can be defined empirically. By the such way experts can define the values of power of electron beam Pb, residual gas pressure pg and the voltage of arc discharge Ud, which are provided the suitable current density jd for maintaining the chemical reaction between the metal vapors and residual gases. As a result of applying the proposed model, the required quality of both standard and novel nanostructurized ceramic films, which can be obtained, is ensuring. For estimation the necessary power of electron beam, the relations (4 – 11), presented at the section 3.2, as well as graphic dependence, given at Fig. 4, can be used. For defining the necessary parameters of HVGDEG, which is generally considered as advanced tool for obtaining the nanostructurized thin ceramics’ films by using physical vapor deposition at the medium of active gases [1 – 4], can be used universal complex model, have been described early in the chapter of book [6]. And for defining the value of arc current density, necessary for maintaining the chemical reaction between the metal vapor and residual gas, the general recommendations, formulated in the papers [1 – 4], are usually used by the experts.
CONCLUSION
The mathematic model, based on the analytical relations, predestined to pervious estimation the distribution of electrical potential and current density at the electron-beam technological systems for reactive chemical vapor deposition, is presented at this chapter of the book. At the second part of chapter the basic principles of formed model have been formulated and main electrical and geometry parameters of simulated arc-discharge electrodes’ system are defined.
At the section 3.1 formulated the basic set of equations for finding the electric potential distribution at the system with the positive potential on the thin ring electrode with inner radius Rr.
At the section 3.2 the main internal thermodynamic parameters of simulated evaporation system, such as pressure of saturated vapors ps, temperature of metal evaporation Tev and the pressure of residual gas pg are considered and analytical relations for calculation the concentration of metals atoms nm and the necessary electron beam power Pb have been proposed. Corresponded graphic dependences nm (Tev) and Pb (Tev) are given at Fig. 3 and Fig. 4.
At the section 3.3 the basic mathematical relations for calculation the arc discharge current density and the space charge at the simulated electrodes’ system have been obtained, at this section of chapter the main analytical transformers, which have been used, are also shown.
At the section 3.4 the electrostatic problem for considered electrodes’ system has been solved by direct integration of Poisson equation at the cylindrical coordinates. The relations for space charge of moving particles, which are always necessary for solving the Poisson equation, have been obtained previously at the section 3.3. Direct integration of the Poisson equation led to obtaining the cubic equation, which have been solved analytically. At the section 3.4 also the main analytical transformers, which have been used, are shown.
At the section 4 the simulation results for the distribution of the electric potential and arc current density at the plain of ring electrode symmetry, obtained with using the presumptions and relations, given at the pervious parts of the chapter, have been presented and analyzed. Graphic dependences U(r) and jd(r), for different voltage of arc discharge maintaining Ud, are given at Fig. 6 and Fig. 7.
The main advantage of proposed model of arc discharge for reactive deposition of nanostructurized ceramic films is its simplicity, because it based only on analytic relations and don’t include iterative numerical calculations. But in any case, it generally corresponded to the main physical principles of electric fields theory [12, 13], thermodynamic and gas dynamic theory [14, 15], as well as to the theory of gas discharges [18 – 20]. Therefore, generally obtained simulation results for distribution of electric field and arc discharge current density at the ring plane are looks plausible. For improving the accuracy of proposed model more precision values of the used semiempirical coefficients C1, C2, C3, K, S1 and S2 can be defined empirically for the specific technology and for metals and gases, applied for obtaining the high-quality nanostructure ceramic films [1 – 4]. Therefore, another advantage of the proposed model is its versatility and the possibility of its’ using for different parameters of the electrode system and for any metals and gases. Certainly, in such case defining of precision values of the semiempirical coefficients is the separate complex and sophisticated problem. For obtaining the approximative values of these coefficients the handbooks on basic physics [17], on physics of gas discharges [18 – 20], as well as on gas dynamics [14 – 16] can be used.
It also should be pointed out, that for realizing the technology of electron-beam deposition of nanostructurized films the HVGDEG can be successfully applied, because the electron guns of such type are reliably and stably operated at the medium of active gases [5 – 8]. For defining the HVGDEG energetic parameters the universal complex model, proposed at the book [6], can be used. In the such situation the proposed early model of HVGDEG and the model of the arc discharge in the metal vapor, complexly described in this chapter, have to be used simultaneously. Therefore, at the practical point of view, these two models can be realized as one integrated software complex.
Basic analytical relations and simulation results, have been considered and analyzed in this chapter, are also very interesting at the practical points of view for the experts at the branch of designing the modern electron beam installations for deposition the nanostructurized ceramic coatings. Furthermore, the proposed model is simple and can be easy used by the experts. Choosing the parameters of technological process of nanostructurized ceramic films deposition is the specific topic of further scientific and applied engineering researches. Therefore, applying of proposed model to the estimation of electric parameters of arc discharge in the metal vapors and active gases can led the experts to the new advanced ideas on creating the high-quality films form nanostructurized ceramics.
REFERENCES
- Feinaeugle P, Mattausch G, Schmidt S, Roegner FH. (2011). A new generation of plasma-based electron beam sources with high power density as a novel tool for high-rate PVD. Society of Vacuum Coaters, 54-th Annual Technical Conference Proceedings, Chicago, pp. 202–209.
- Mattausch G, Zimmermann B, Fietzke F, Heinss JP, Graffel B, et al. (2014). Gas discharge electron sources – proven and novel tools for thin-film technologies. Elektrotechnica and Electronica (E+E). 49(5-6):183–195.
- Grechanyuk MI, Melnyk AG, Grechanyuk IM, et al. (2014). Modern electron beam technologies and equipment for melting and physical vapor deposition of different materials. Elektrotechnica and Electronica (E+E). 49(5-6):115–121.
- Mattausch G, Scheffel B, Zywitzki O, Metzner C, Roegner FH. (2012). Technologies and tools for the plasma-activated EB high-rate deposition of Zirconia. Elekctrotechnica and Electronica (E+E). 47(5-6):152–158.
- Denbnovetskiy S, Melnyk V, Tugai B, Tuhai S, Wojcik W, et al. (2017). Principles of operation of high voltage glow discharge electron guns and particularities of its technological application. Proceedings of SPIE, The International Society of Optical Engineering, pp. 10445 – 10455.
- Melnyk I, Tuhai S, Pochynok A. (2021). Universal Complex Model for Estimation the Beam Current Density of High Voltage Glow Discharge Electron Guns. Lecture Notes in Networks and Systems, 152, Springer, pp. 319-341.
- Denbnovetsky SV, Melnyk IV, Melnyk VG, Tugai BA, Tuhai SB. (2017). Simulation of Dependences of Discharge Current of High Voltage Glow Discharge Electron Guns From Parameters of Electromagnetic Valve. IEEE 37-th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, Conference proceedings, pp. 369–374.
- Melnyk IV. (2017). Simulation of Energatic Efficiency of Triode High Voltage Glow Discharge Electron Sources Account of Temperature of Electrons and Its’ Mobility in Anode Plasma. Radioelectronics and Communication Systems. 60(7):413–424.
- Zakharov A, Litvintsev S, Ilchenko M. (2020). Trisection Bandpass Filter with Mixed Cross-Coupling and Different Paths for Signal Propagation. IEEE Microwave Wireless Components Letters. 30(1):12-15.
- Zakharov A, Litvintsev S, Ilchenko M. (2019). Trisection Bandpass Filters with All Mixed Couplings", IEEE Microwave Wireless Components Letters. 29(9):592-594.
- Zakharov A, Litvintsev S, Ilchenko M. (2020). Transmission Line Tunable Resonators with Intersecting Resonance Regions. IEEE Transaction on Circuits System, II, Experimental Briefs, 67(4):660-664.
- Shadowitz A. (2010). The Electromagnetic Field, New-York: Dover Publications Inc., pp. 768.
- Schwartz M. (2003). Principles of Electrodynamics. New-York: Dover Publications Inc., pp. 368.
- Zucker RD, Biblarz O. (2019). Fundamentals of Gas Dynamics, 3rd Edition. John Wiley and Sons, pp. 560.
- Rathakrishnan E. (2015). High Enthalpy Gas Dynamics. John Wiley and Sons, pp. 330.
- James EAJ, Keith TG. (2006). Gas Dynamics. Pearson Prentice Hall, pp. 672.
- Kuchling H. (2014). Taschenbuch der Physik [Handbook on Physics]. Hanser Verlag, 21 Edition, (in German), pp. 711.
- Smirnov BM. (2015). Theory of Gas Discharge Plasma. Springer, pp. 433.
- Lieberman MA, Lichtenberg AJ. (1994). Principles of Plasma Discharges for Materials Processing. New York: Wiley Interscience, pp. 572.
- Raizer Yu P. (1991). Gas Discharge Physics. New York: Springer, pp. 449.
- Mathews JH, Fink KD. (1998). Numerical Methods. Using Matlab. Third Edition, Print Hall, Amazon, pp. 336.
- Bronshtein IN, Semendiaev KA. (1986). Spravochnik po matematike. Dlia inzhenerov i uchaschihsia vtuzov. [Handbook on Mathematic for Engineers and Students of Higher Technical Institutions]. Moscow: Nauka, GRFML Edition, (in Russian), pp. 544.
 Abstract
Abstract  PDF
PDF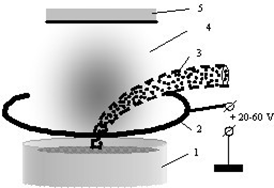
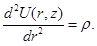
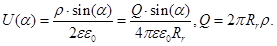
.png)
.png)
.png)
.png)
.png)
.png)
.png)
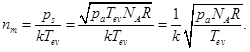
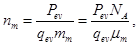


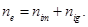
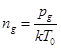
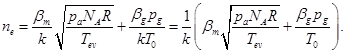
.png)
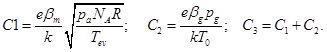
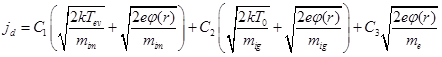
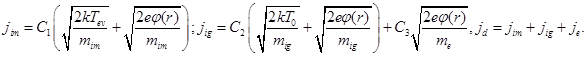
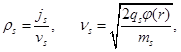
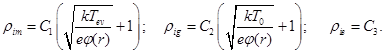

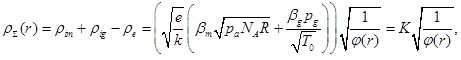
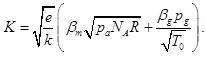

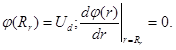

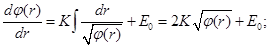
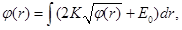


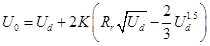
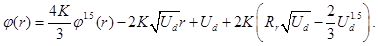
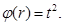

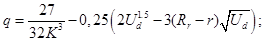
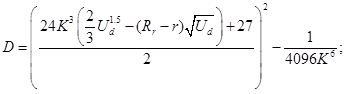
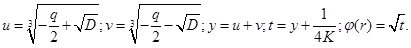
.png)